This post is for the nerds. Do you like math?
Mortorious used several digital “death counters” to show the estimated number of deaths that occurred somewhere in the United States by a various causes during Burning Man 2019. Since we wanted each of the death counters to increment at an appropriate rate, but we also wanted to avoid the distraction of unrealistic uniformity, the control of the death counters incorporated randomness.
The PDF below documents three mathematical aspects of the Mortorious project’s death counters, each represented by an equation.
- How to model the times between deaths using an exponential distribution:
(1) 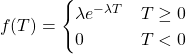
- How to generate exponentially distributed pseudorandom numbers using a uniform pseudorandom number generator:
(2) ![]()
- How to put an upper limit on exponentially distributed pseudorandom numbers by solving a seemingly simple but quite difficult equation:
(3) ![]()
Here’s the full PDF.
