You are here: Home / Dome / Strengths of Materials (Part 1)

Strengths of Materials (Part 1)

May 12, 2005 by

I find things in unexpected places. On the exhibit floor of the National Association of Broadcasters convention, while walking past the booth of Music Books Plus, I discovered the most amazing and readable book on structural analysis: Structural Design for the Stage (now in its 2nd edition). It presents nearly everything that I need to analyze the strength of the materials in a dome.

Allowable Strength Design

Engineers design in a “safety factor” by specifying materials that are stronger than theory requires. The safety factor ensures that a design is safe even with variation in materials (such as wood).

In “allowable strength design” the safety factor is determined by manufacturers’ associations and code officials. Engineers just need to compare the actual stress with the allowable stress for each material in the design. As long as all actual stresses are less than the corresponding allowable stresses, the design is safe. (At least as far as materials strengths are concerned.)

So to evaluate the strength of the dome design, I need to look at the strengths of bolts, plates, and 2×4s.

Strength of Bolts

If the bolts in the dome were to fail, it would be through shearing. So just how much shearing load is allowed in the bolts? The dome will use 5/16-inch, 18 thread-per-inch steel bolts. The smallest circular cross section of these bolts has a diameter of 0.236 in. The allowable shear stress for steel, Fv, is 10,000 psi. What is the allowable shearing load?

    \begin{eqnarray*} P_{allowable}&=&F_v \mbox{ Area} = 10,000 \mbox{ Area}\\ \mbox{Area}&=&\frac{1}{4} \pi D^2 = \frac{1}{4} \pi \times 0.236^2 = 0.0437 \mbox{ in}^2\\ P_{allowable}&=&437 \mbox{ pounds} \end{eqnarray*}

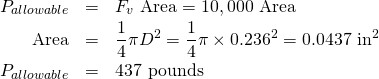
Strength of Joint Plates

Joint plates will be made from 16-gauge, 14-gauge, or 12-gauge sheet steel. Given the strength of the bolt, above, and assuming that the joint plates should be as strong as the bolts, it’s possible to solve for the required backsets of the holes in the plates for various thicknesses of plates.

Since the bolts and the plates are made from the same material and have the same allowable shearing load, the total cross sectional area of both is the same. Realize, however, that tearing through the bolt hole requires shearing the metal on either side of the hole, and so the total shear area is twice what one would otherwise expect, meaning the backset can be halved.

    \begin{eqnarray*} \mbox{Area}&=&0.0437 \mbox{ in}^2\\ \mbox{Thickness}_{16-gauge}&=&0.060 \mbox{ in}\\ \mbox{Thickness}_{14-gauge}&=&0.075 \mbox{ in}\\ \mbox{Thickness}_{12-gauge}&=&0.105 \mbox{ in}\\ \mbox{Backset}&=&\frac{1}{2} \times \frac{\mbox{Area}}{\mbox{Thickness}}\\ \mbox{Backset}_{16-gauge}&=&\frac{1}{2} \times \frac{0.0437}{0.060} = 0.36 \mbox{ in}\\ \mbox{Backset}_{14-gauge}&=&\frac{1}{2} \times \frac{0.0437}{0.075} = 0.29 \mbox{ in}\\ \mbox{Backset}_{12-gauge}&=&\frac{1}{2} \times \frac{0.0437}{0.105} = 0.21 \mbox{ in} \end{eqnarray*}

Strength of 2×4s

The 2×4 members can be in either compression or tension, and they will need to resist bending. So three separate analyses anre needed. That will be in Part 2.

Filed Under: Dome Tagged With: